혼돈 이론

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요
2. 정의
3. 성질
4. 응용
5. 역사
참조

1. 개요

혼돈 이론은 초기 조건에 민감하고, 위상 혼합성을 보이며, 조밀한 주기적 궤도를 갖는 동역학계인 혼돈계에 대한 연구이다. 초기 조건의 작은 변화가 결과에 큰 차이를 가져오는 '나비 효과'가 특징이며, 로버트 데바니의 정의에 따르면 초기 조건에 민감하고, 위상적으로 추이적이며, 밀집된 주기 궤도를 가져야 혼돈으로 분류된다. 혼돈계는 3차원 이상에서 발생하며, 이산 시간 동역학계에서는 차원 제약이 없다. 혼돈 운동은 프랙털 구조의 야릇한 끌개를 가지며, 공존하는 끌개가 존재할 수 있다. 혼돈 이론은 기상, 지질학, 생물학, 경제학 등 다양한 분야에 응용되며, 암호학, 로봇 공학, 생물학, 경제 모델, 교통 예측 등에서 활용된다. 혼돈 이론은 19세기 푸앵카레의 삼체 문제 연구에서 시작되어, 20세기 후반 로렌츠의 날씨 예측 연구, 망델브로의 프랙탈 기하학 연구를 거쳐 대중화되었다.

더 읽어볼만한 페이지

혼돈 이론 - 창발
창발은 부분에는 없던 성질이 전체에서 나타나는 현상으로, 철학적으로는 요소의 속성으로 설명할 수 없는 체계의 특징을 의미하며, 복잡계 과학, 생명 현상 등 다양한 분야에서 중요한 개념으로 다뤄진다.
혼돈 이론 - 난류 (역학)
난류는 유체의 불규칙하고 무작위적인 운동 상태로, 일상생활과 공학 등 다양한 분야에서 관찰되며 여러 특징을 설명하기 위한 연구가 진행 중이다.

혼돈 이론
지도 정보
기본 정보
분야	수학 및 과학
기반	비선형계 및 초기 조건
관련 개념	나비 효과 프랙털 어트랙터 비선형 동역학
주요 특징
민감성	초기 조건에 대한 민감성
예측 불가능성	장기 예측의 어려움
결정론적	결정론적 시스템에서 발생 가능
역사
초기 연구	에드워드 로렌츠의 기상 모델 연구 (1960년대)
발전	로렌츠 방정식 로지스틱 사상
용어 사용	1970년대에 '혼돈'이라는 용어 사용 시작
응용 분야
물리학	유체 역학, 양자 역학, 천체 역학
기상학	기상 예측
생물학	생태계 모델링, 신경과학
경제학	금융 시장 분석
사회과학	사회적 현상 분석
공학	제어 시스템, 로봇 공학
의학	심장 박동 분석, 뇌파 분석
주요 학자
관련 개념 추가 설명
나비 효과	초기 조건의 작은 변화가 시간이 지남에 따라 큰 차이를 만들 수 있음.
로렌츠 끌개	로렌츠 시스템에서 나타나는 혼돈적 특성을 보여주는 어트랙터
로지스틱 사상	혼돈 현상을 보여주는 간단한 수학적 모델
혼돈 이론의 정의
정의	현재가 미래를 결정하지만, 근사적인 현재가 미래를 근사적으로 결정하지 못하는 현상.
비선형성	비선형적인 시스템에서 주로 나타나는 현상.
추가 정보
참고 문헌	브리태니커 백과사전 - 혼돈 이론 프랙털 재단 - 혼돈 이론이란? 매스월드 - 혼돈 제프 보잉 - 혼돈 이론과 로지스틱 사상 에드워드 로렌츠 - 혼돈의 본질 크리스 피오트로프스키 - 코로나19 팬데믹과 혼돈 이론 데이비드 와인버거 - 일상의 혼돈 스탠포드 철학 백과사전 - 혼돈
관련 서적	스티븐 H. 켈러트 - 혼돈의 여파 블라디미르 G. 이반세비치 - 복잡한 비선형성 마크 S. 모스코, 프랭크 H. 데이먼 - 혼돈의 질서에 관하여
학술 논문	보웬 셴, 로저 A. 피엘케 외 - 로렌츠 모델 내의 세 가지 나비 효과 샬럿 베른들 - 예측 불가능성에 대한 혼돈의 새로운 의미는 무엇인가? 크리스토퍼 M. 댄포스 - 벽에 걸린 대기 속의 혼돈

2. 정의

동역학계가 다음 세 가지 성질을 만족하면 혼돈계라고 한다.^[169]^[170]

초기 조건에 민감해야 한다. 즉, 초기 조건의 작은 변화가 결과에 큰 차이를 만든다.
위상 혼합성을 보인다.
조밀한 주기적 궤도들을 가진다.

각 조건에 대한 구체적인 정의는 다음과 같다.

'''초기 조건에 민감'''하다는 것은 랴푸노프 지수가 양수라는 뜻이다. 랴푸노프 지수가 양수이면, 계의 시간 변화는 초기 조건에 지수적으로 의존한다. 이는 나비 효과로 흔히 불리며, 혼돈계의 주요 성질로 여겨지지만, 초기 조건에 대한 민감성은 혼돈계를 정의하는 세 가지 조건 중 하나일 뿐이다. 예를 들어,

x\mapsto 2x

는 초기 조건에 민감하지만 혼돈적이지 않다.

'''위상 혼합성'''이란 위상 공간

X

위의 자기 연속 함수

f\colon X\to X

로 주어지는 이산 시간 동역학계

:

x_{n+1}=f(x_n)

에서, 임의의 열린집합

U,V\subseteq X

에 대하여, 다음 조건을 만족시키는 자연수

N_{U,V}\in\mathbb N

가 존재하면, 이 이산 시간 동역학계가 위상 혼합성을 보인다고 한다.

:

\forall n\ge N_{U,V}\colon f^n(U)\cap V\ne\varnothing

즉,

N_{U,V}

이상의 시간이 지나면,

U

의 시간 변화는

V

와 서로 섞이게 된다. 마찬가지로, 연속 시간 동역학계

:

x\mapsto\phi_t(x)\qquad(t\in\mathbb R_{\ge0})

의 경우,

:

\forall t\ge T_{U,V}\colon\phi_t(U)\cap V\ne\varnothing

가 되는 시간

T_{U,V}\in\mathbb R_{\ge0}

이 존재해야 한다.

동역학계의 '''궤도'''는 주어진 초기 조건의 시간 변화들로 구성된 부분 집합이다. '''주기적 궤도'''는 궤도 가운데, 일정한 시간이 지나면 원점으로 돌아오는 것이다. '''조밀한 주기적 궤도들'''을 갖는다는 것은 모든 주기적 궤도들의 합집합이 조밀 집합을 이룬다는 것이다. 즉, 모든 초기 조건에 대하여, 이에 대하여 임의적으로 가까운 주기적 궤도가 존재한다.

로버트 L. 데바니가 제시한 정의에 따르면, 동역학계를 혼돈으로 분류하려면 다음과 같은 특성을 가져야 한다.^[22]

# 초기 조건에 민감해야 한다.

# 위상적으로 추이적이어야 한다.

# 밀집된 주기 궤도를 가져야 한다.

구간으로 주의를 제한하면 두 번째 속성이 다른 두 속성을 의미한다.^[26] 혼돈에 대한 대안적이고 일반적으로 더 약한 정의는 위 목록의 처음 두 속성만을 사용한다.^[27]

3. 성질

일반적으로 "혼돈"은 "무질서 상태"를 의미한다.^[20]^[21] 그러나 혼돈 이론에서는 이 용어가 더 정확하게 정의된다. 혼돈에 대한 보편적으로 받아들여지는 수학적 정의는 없지만, 로버트 L. 데바니가 제시한 정의에 따르면, 동역학계를 혼돈으로 분류하려면 다음과 같은 특성을 가져야 한다.^[22]

# 초기 조건에 민감해야 한다.

# 위상적으로 추이적이어야 한다.

# 밀집된 주기 궤도를 가져야 한다.

위의 마지막 두 가지 특성은 초기 조건에 대한 민감성을 의미하는 것으로 나타났다.^[23]^[24] 이산 시간의 경우, 이는 연속적인 사상의 모든 메트릭 공간에 대해 사실이다.^[25]

구간으로 주의를 제한하면 두 번째 속성이 다른 두 속성을 의미한다.^[26] 혼돈에 대한 대안적이고 일반적으로 더 약한 정의는 위 목록의 처음 두 속성만을 사용한다.^[27]

초기 x 위치에 대한 민감도를 보여주는 사상. x와 y 값의 두 시리즈는 미세한 초기 차이로 인해 시간이 지남에 따라 현저하게 발산한다.

'''초기 조건에 대한 민감성'''은 혼돈 시스템의 각 지점이 미래 경로 또는 궤적이 크게 다른 다른 지점에 의해 임의로 근접하게 근사된다는 것을 의미한다. 따라서 현재 궤적의 임의로 작은 변화 또는 변동은 미래 행동에 상당히 다른 결과를 초래할 수 있다.^[3]

초기 조건에 대한 민감성은 "나비 효과"로 알려져 있다. 이는 1972년 에드워드 로렌츠가 발표한 논문 제목 ''예측 가능성: 브라질에서 나비의 날갯짓이 텍사스에서 토네이도를 일으킬까?''에서 유래되었다.^[28] 날갯짓하는 나비는 시스템의 초기 조건에 대한 작은 변화를 나타내며, 이는 대규모 현상의 예측 가능성을 방해하는 일련의 사건을 야기한다.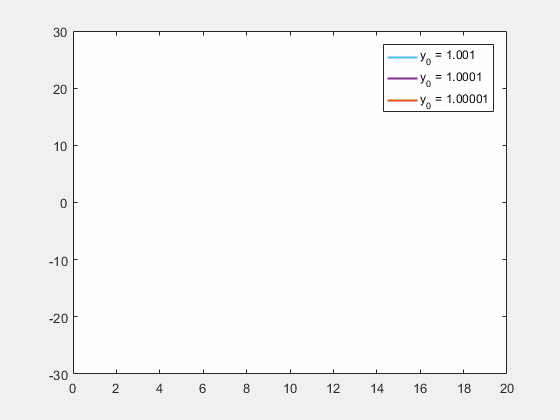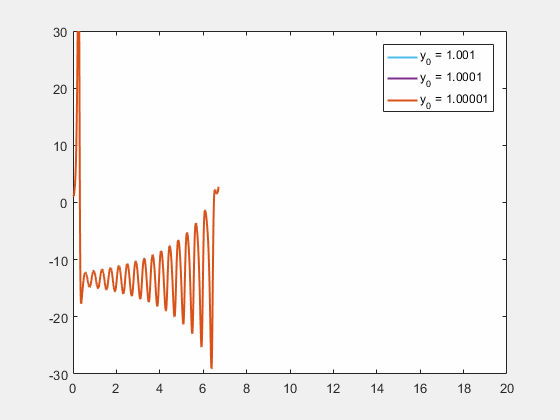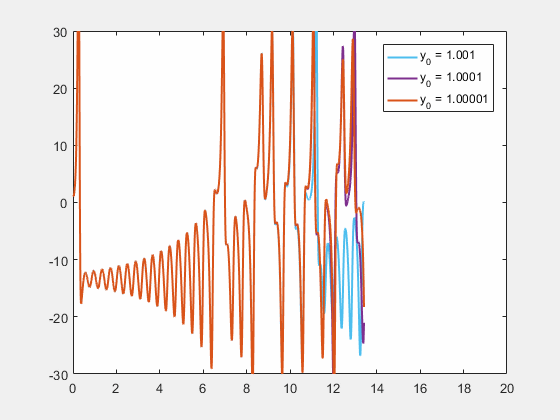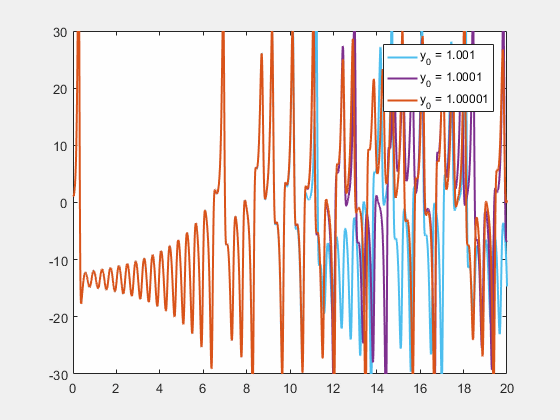

로렌츠 방정식을 사용하여 y 변수에 대한 플롯을 생성. x와 z의 초기 조건은 동일하게 유지되었지만 y의 초기 조건은 1.001, 1.0001 및 1.00001로 변경. 초기 값의 아주 작은 차이라도 약 12초 후 상당한 변화를 야기한다.

로렌츠는 "민감한 의존성은 카오스의 허용 가능한 정의로 사용될 수 있습니다"라고 제안했다.^[6] 또한 나비 효과를 "동역학 시스템의 상태에 대한 작은 변화가 그 후의 상태를 변화 없이 뒤따랐을 상태와 크게 다르게 만들 것입니다."라고 정의했다.^[6]

초기 조건에 대한 민감성의 결과는 시스템에 대한 정보가 제한된 경우, 특정 시간 이후에는 시스템이 더 이상 예측 불가능해진다는 것이다. 날씨는 약 1주일 앞만 예측 가능하다.^[30] 예를 들어, 지구 표면 온도가 자연적으로 100°C에 도달하거나 -130°C 이하로 떨어지지 않을 것임을 알지만, 가장 더운 날이 정확히 언제가 될지는 예측할 수 없다.

리아푸노프 지수는 초기 조건에 대한 민감성을 초기 조건의 방해로부터의 지수 발산 속도의 형태로 측정한다.^[31]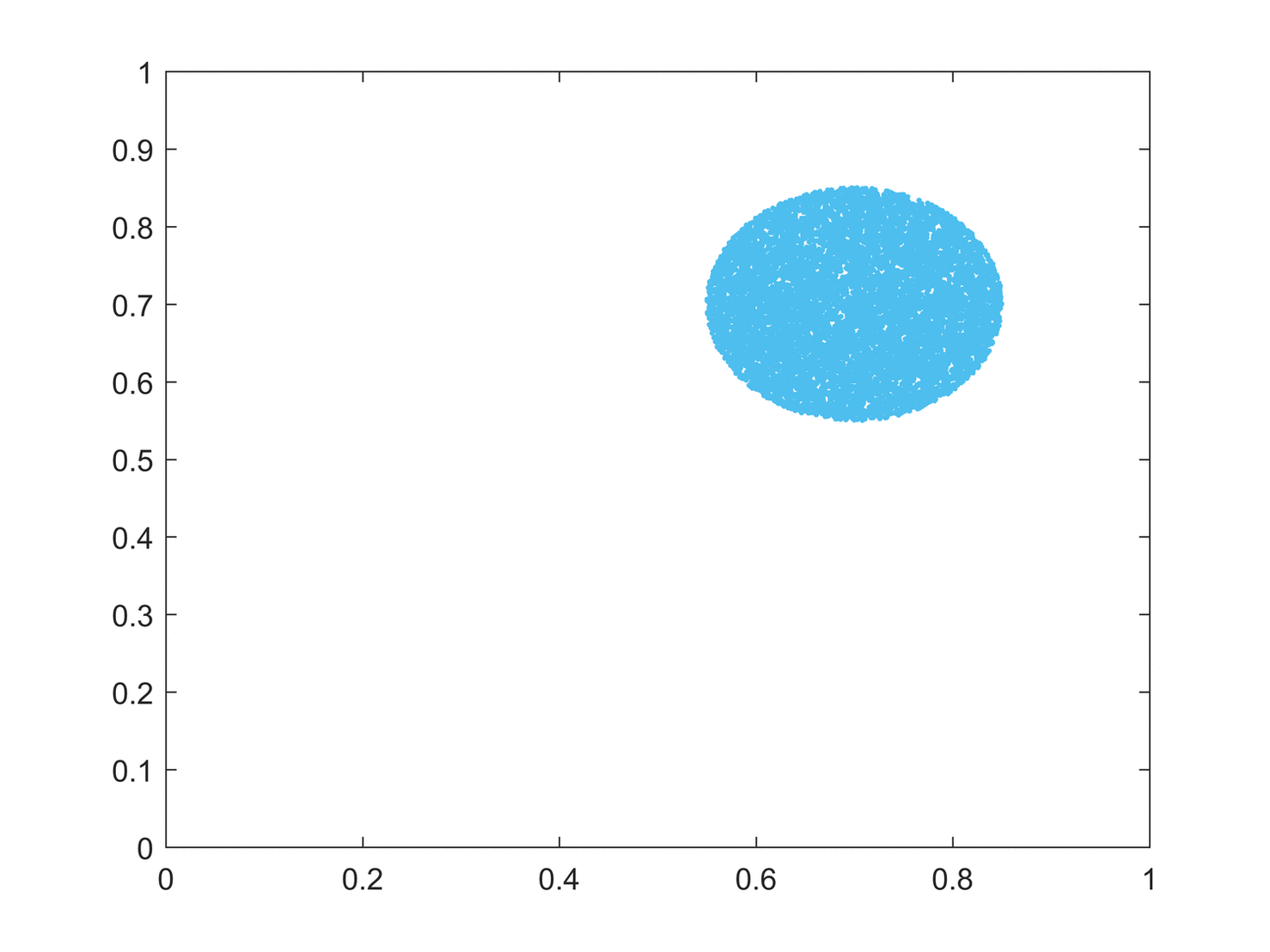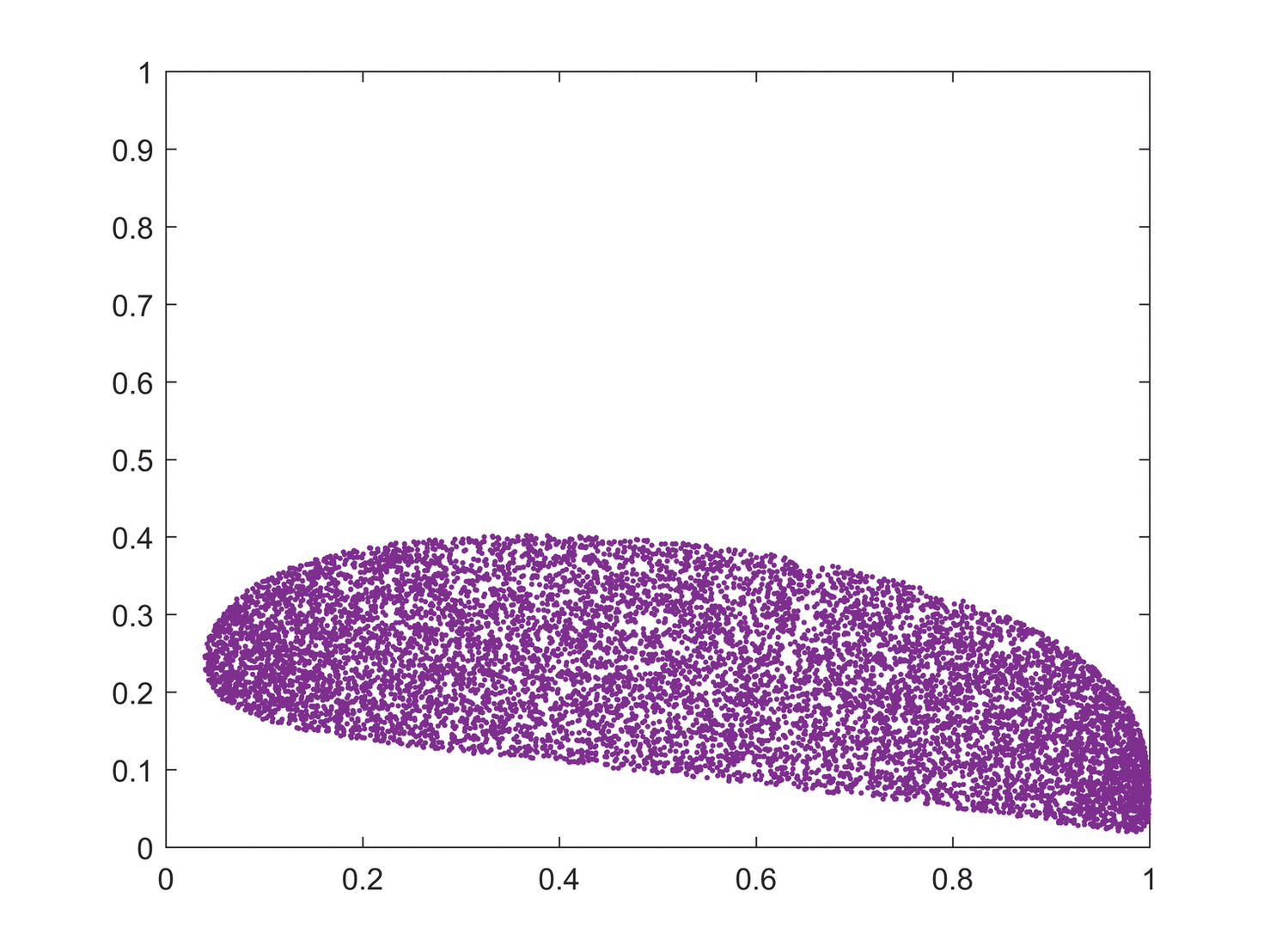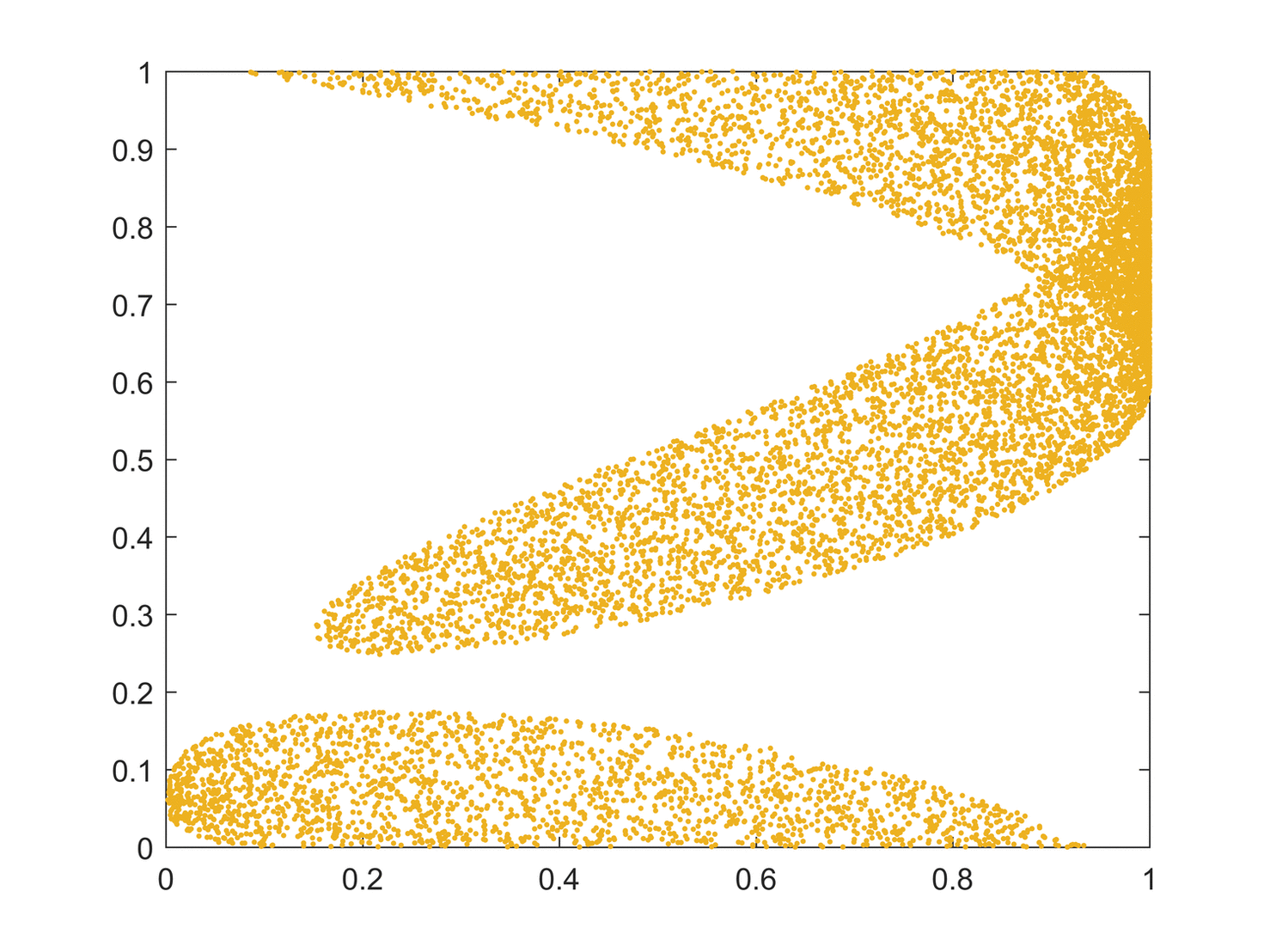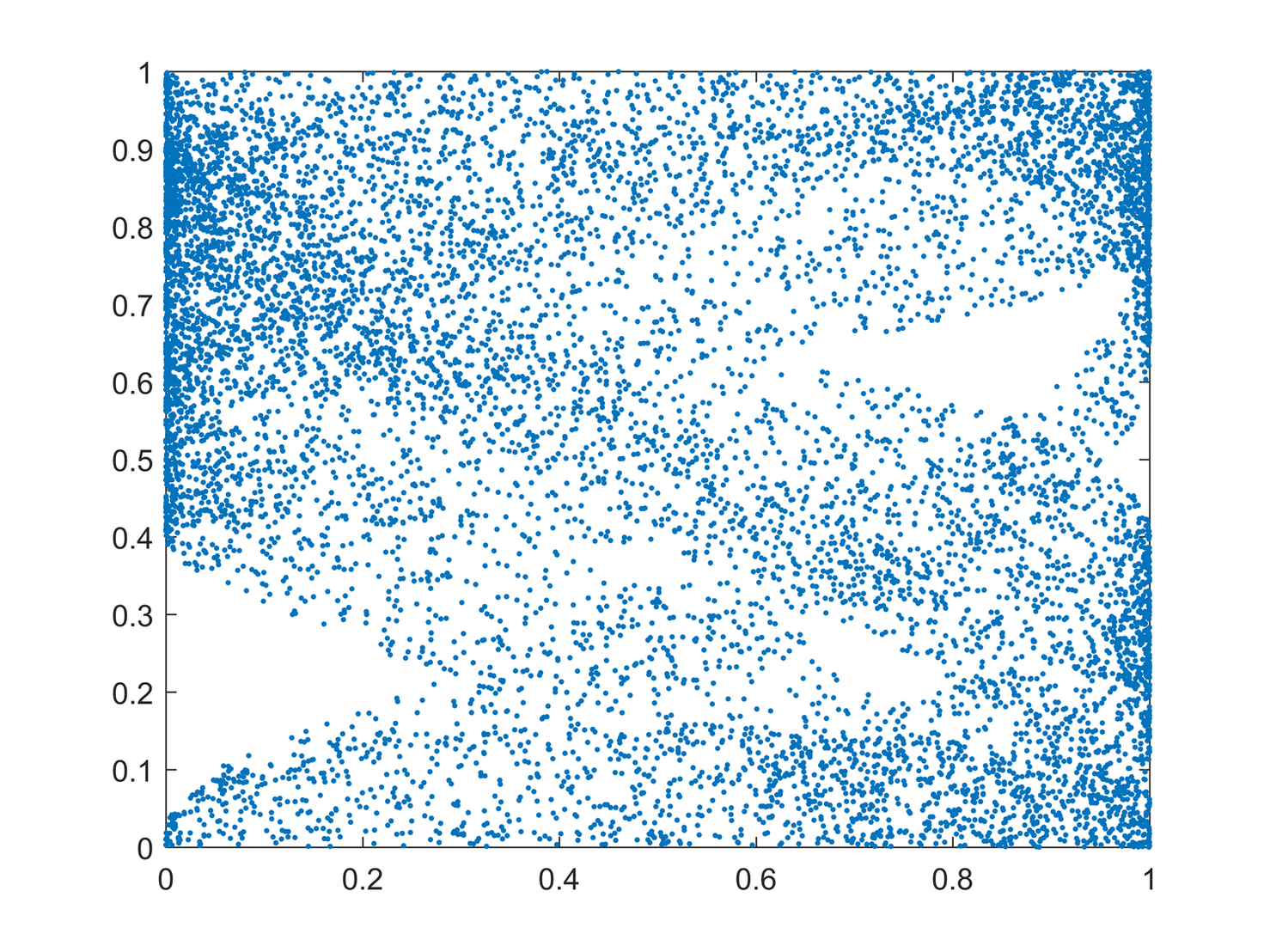

상태 집합 [x,y]를 로지스틱 사상에 통과시킨 6회 반복. 첫 번째 반복(파란색)은 초기 조건이며, 원을 형성한다. 반복이 진행됨에 따라 "혼합"이 발생한다.

위상 혼합(또는 위상적 추이성)은 시스템이 시간에 따라 진화하여 주어진 임의의 영역 또는 열린 집합이 위상 공간의 다른 임의의 영역과 결국 겹친다는 것을 의미한다. "혼합"의 개념은 색깔 있는 염료 또는 유체의 혼합과 같은 혼돈 시스템의 예이다.

위상 혼합은 종종 초기 조건에 대한 민감성만으로 혼돈을 동일시하는 설명에서 생략된다.

함수

f:X \to X

가 위상적으로 추이적이라는 것은, 공집합이 아닌 임의의 두 열린 집합

U, V \subset X

에 대해,

f^{k}(U) \cap V \neq \emptyset

인

k > 0

이 존재하는 경우를 말한다. 위상적 추이성은 위상적 혼합보다 약한 조건이다. 어떤 함수가 위상적으로 추이적이라면, 점 ''x''와 영역 ''V''이 주어졌을 때, 궤도가 ''V''를 통과하는 ''x'' 근처의 점 ''y''가 존재한다. 이는 시스템을 두 개의 열린 집합으로 분해할 수 없다는 것을 의미한다.^[32]

카오스 시스템에서 밀집된 주기 궤도를 갖는다는 것은 공간의 모든 점이 주기 궤도에 임의로 가까이 접근한다는 것을 의미한다.^[32] 1차원 로지스틱 사상은 주기 궤도의 밀도를 갖는 가장 간단한 시스템 중 하나이다.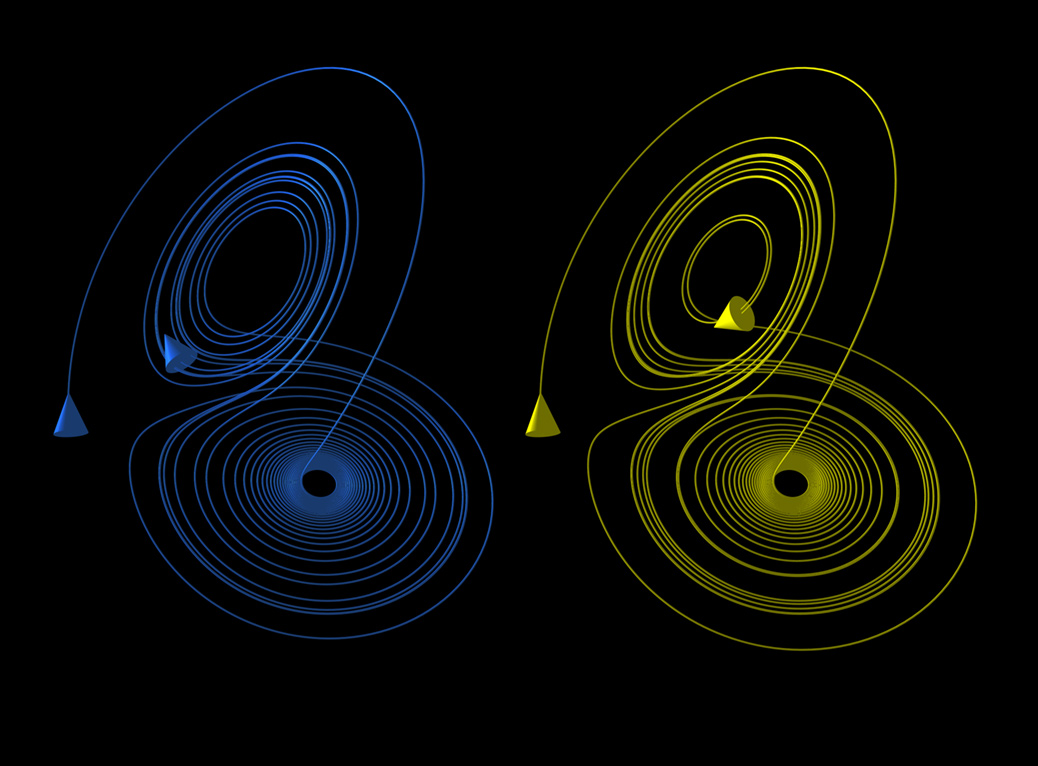

로렌츠 아tractor는 혼돈적인 거동을 보여준다. 두 그림은 아tractor가 차지하는 상공간 영역 내에서 초기 조건에 대한 민감한 의존성을 보여준다.

일부 동역학계는 어디에서나 혼돈적이지만, 많은 경우 혼돈적 거동은 상공간의 부분 집합에서만 발견된다. 혼돈적 거동이 아tractor에서 발생하는 경우, 많은 초기 조건 집합이 이 혼돈 영역으로 수렴하는 궤도를 생성한다.^[36]

혼돈적 아tractor를 시각화하는 쉬운 방법은 아tractor의 인력 분지에 있는 점으로 시작하여 그 후속 궤도를 그리는 것이다. 위상적 추이성 조건 때문에 전체 최종 아tractor의 그림을 생성할 가능성이 높다. 오른쪽 그림의 두 궤도는 로렌츠 아tractor의 일반적인 모양을 보여준다. 이 아tractor는 로렌츠의 기상 시스템에 대한 3차원 모델에서 비롯된다.

고정점 아tractor 및 극한 순환과 달리 혼돈 시스템에서 발생하는 아tractor(스트레인지 아tractor)는 매우 상세하고 복잡하다. 스트레인지 아tractor는 연속 동역학계와 이산 시스템 모두에서 발생한다. 줄리아 집합은 스트레인지 반발자로 생각할 수 있다. 스트레인지 아tractor와 줄리아 집합 모두 프랙탈 구조를 가지며, 프랙탈 차원을 계산할 수 있다.

초기 상태가 주어지면 이후 상태량의 변화가 결정되는 계를 동역학계라고 한다. 결정론적 동역학계를 다룬다는 점을 강조하여 결정론적 동역학계라고도 한다. 카오스 이론에서 연구되는 카오스는 결정론적 동역학계에 따라 만들어진다. 카오스 이론이 다루는 카오스를 '''결정론적 카오스'''라고 부른다.

카오스 이론에서 카오스의 엄밀한 정의는 연구자에 따라 다르며, 통일된 정의는 없다. 카오스의 정의는 「비선형적인 결정론적인 동역학계에서 발생하는, 초기값 민감성을 가진, 유계인 비주기 궤도」라고 할 수 있다. 이러한 궤도를 포함하는 동역학계의 성질을 카오스라고도 한다. 궤도를 가리키는 것을 명확히 하기 위해 '''카오스 궤도'''라고 부른다.

카오스의 특성으로 언급되는 것이 '''초기값 민감성'''이다. 같은 계라도 초기 상태에 아주 작은 차이가 있으면, 시간이 지남에 따라 지수 함수적으로 그 차이가 커지는 성질이다. 이 성질은 '''궤도 불안정성'''이라고도 한다. 정량적으로는 리아푸노프 지수, 콜모고로프-시나이 엔트로피 등으로 평가된다.

초기값 민감성으로 인해 작은 차이도 지수 함수적으로 증가하기 때문에, 초기값 민감성을 지닌 실제 계의 미래 예측은 어렵다. 초기 상태의 측정 오차를 없앨 수 없으므로, 장시간 후의 상태 예측은 불가능하다. 이러한 성질은 '''장기 예측 불가능성'''이나 '''예측 불가능성''' 등으로 불린다. 단시간 내라면 유용한 예측이 가능하다. 이러한 성질은 '''나비 효과'''라고 불린다.

카오스의 수학적 정의로 로버트 데바니의 정의가 있다.

다음 세 가지 조건을 만족하는 사상 ''f'': ''V'' → ''V''는 ''V'' 위에서 카오스적이다.

# 초기 조건에 민감하게 의존한다.

# 위상적으로 추이적이다.

# 주기점은 ''V''에서 밀집되어 있다.

3. 1. 차원

푸앵카레-벤딕손 정리에 따르면, 연속 시간 동역학계에서 2차원 이하의 계는 혼돈을 보일 수 없다. 따라서 혼돈계는 3차원 이상이어야 한다.

이산 시간 동역학계는 이러한 제약이 없다. 예를 들어 로지스틱 사상은 적절한 매개 변수에서 1차원 이산 시간 혼돈계이다.

3. 2. 샤르코우스키 정리와 리-요크 정리

리-요크 정리^[171]에 따르면, 주기 3의 궤도를 갖는 1차원 이산 시간 동역학계는 리-요크 혼돈 현상을 보인다.

이와 관련된 샤르코우스키 정리^[172]는 올렉산드르 미콜라요비치 샤르코우스키가 1964년에 증명한 것으로, 리-요크 정리보다 더 일반적인 내용을 다룬다. 샤르코우스키 정리는 1차원 이산 시간 동역학계의 주기성에 대한 정보를 제공한다.

3. 3. 끌개

혼돈 운동은 위상도에서 야릇한 끌개라는 복잡한 기하학적 구조를 보인다. 야릇한 끌개는 프랙털 구조를 가지며, 종종 비정수 차원을 갖는다. 로렌즈의 기상계를 본뜬 단순한 3차원 모형은 유명한 로렌즈 끌개를 보인다. 로렌즈 끌개는 최초의 끌개 그림 중 하나이자 가장 복잡한 끌개 그림 중 하나이며, 나비의 날개 같은 흥미로운 형태를 보인다.^[36] 또 다른 끌개로 로지스틱 본뜨기처럼 주기배증의 혼돈경로를 따르는 뢰슬러 본뜨기가 있다.

3. 4. 공존하는 끌개

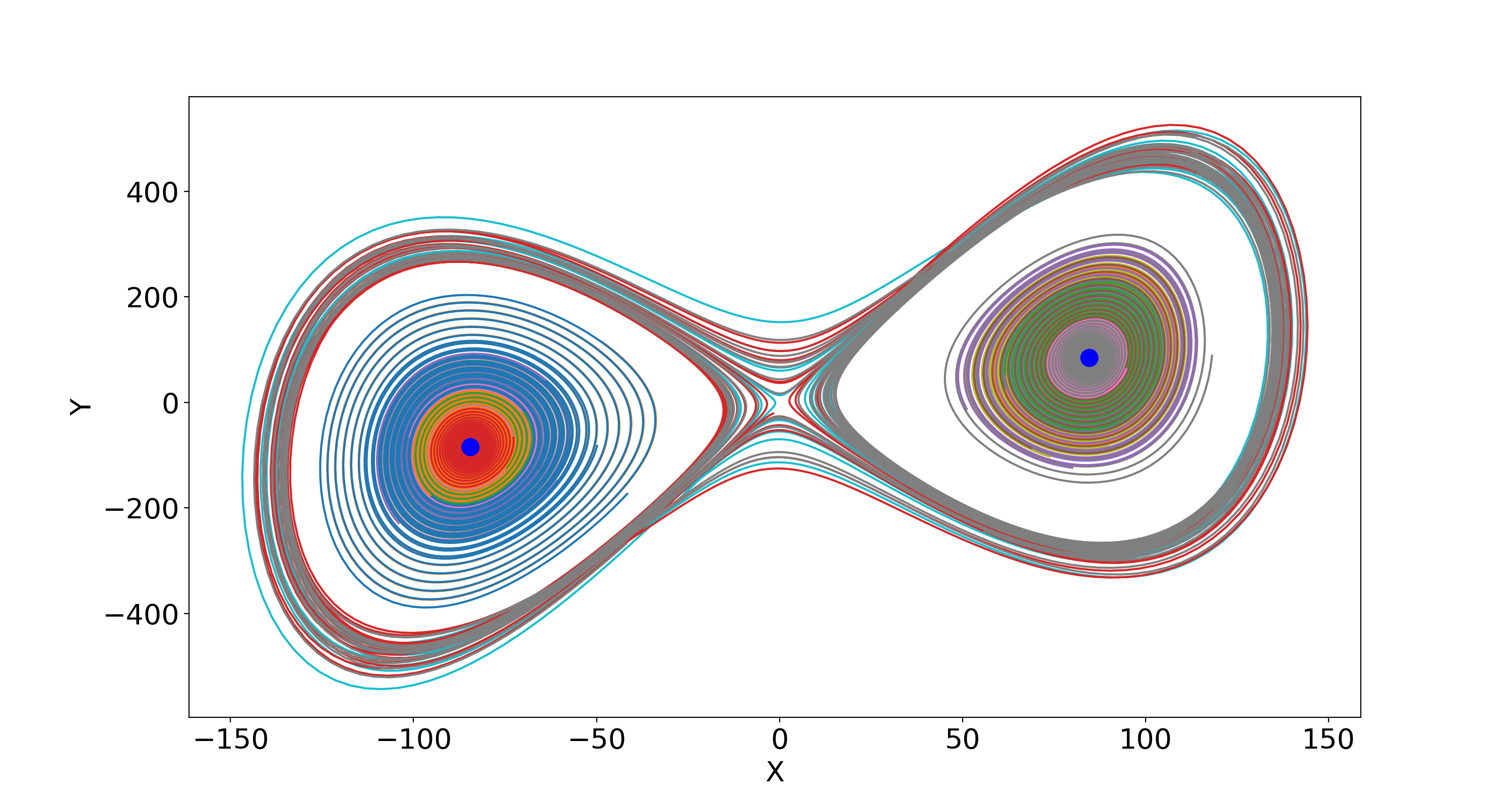
단일 유형의 카오스적 해와는 대조적으로, 최근 로렌츠 모델을 사용한 연구^[37]^[38]는 다양한 유형의 해를 고려하는 것이 중요함을 강조했다. 예를 들어, 동일한 모델링 구성이지만 다른 초기 조건을 사용하는 동일한 모델(예: 이중 진자) 내에서 카오스적 현상과 비카오스적 현상이 공존할 수 있다. 고전적 및 일반화된 로렌츠 모델^[48]^[49]^[39]에서 얻은 끌개 공존의 결과는 "전체 기상 현상은 예측 가능성이 다른 카오스와 질서의 이중적인 특성을 지닌다"는 수정된 견해를 제시했는데, 이는 기존의 "날씨는 카오스적이다"라는 견해와는 대조적이다.

3. 5. 혼돈 시스템의 최소 복잡성

푸앵카레-벤딕손 정리에 따르면, 연속 시간 동역학계에서는 2차원 이하의 계는 혼돈을 보일 수 없다. 즉, 혼돈계는 3차원 이상이어야 한다.

반면, 이산 시간 동역학계의 경우 이러한 제약이 없다. 예를 들어, 적절한 매개 변수를 갖는 로지스틱 사상은 1차원 이산 시간 혼돈계이다.

유한 차원 선형 시스템은 혼돈적일 수 없다. 동역학계가 혼돈적 거동을 보이려면 비선형이거나 무한 차원이어야 한다.

이산적인 혼돈계는 그 차원에 관계없이 야릇한 끌개를 나타낼 수 있다. 반면에 연속 동역학계의 경우 푸앵카레-벤딕손 정리는 야릇한 끌개가 3차원 이상에서만 발생할 수 있음을 보여준다.

3. 6. 무한 차원 사상

결합된 이산 사상의 직접적인 일반화^[50]는 공간적으로 분포된 사상 간의 상호 작용을 매개하는 콘볼루션 적분을 기반으로 한다.

:

\psi_{n+1}(\vec r,t)  = \int K(\vec r - \vec r^{,},t) f [\psi_{n}(\vec r^{,},t) ]d {\vec r}^{,}

여기서 커널

K(\vec r - \vec r^{,},t)

는 관련 물리 시스템의 그린 함수로 유도된 전파자^[51]이며,

f [\psi_{n}(\vec r,t) ]

는 로지스틱 사상과 유사한

\psi \rightarrow G \psi [1 - \tanh (\psi)]

또는 복소 사상이 될 수 있다. 복소 사상의 예로는 줄리아 집합

f[\psi] = \psi^2

또는 이케다 사상

\psi_{n+1} = A + B \psi_n e^{i (|\psi_n|^2 + C)}

이 있다. 파장

\lambda=2\pi/k

을 가진 거리

L=ct

에서의 파동 전파 문제를 고려할 때, 커널

K

는 슈뢰딩거 방정식의 그린 함수 형태를 가질 수 있다.^[52]^[53]

:

K(\vec r - \vec r^{,},L)  = \frac {ik\exp[ikL]}{2\pi L}\exp[\frac {ik|\vec r-\vec r^{,}|^2}{2 L} ]

3. 7. Jerk 시스템

물리학에서 가속도의 시간변화율(Jerk)은 시간에 대한 위치의 3차 도함수이다. 따라서 다음과 같은 형태의 미분 방정식

::

J\left(\overset{...}{x},\ddot{x},\dot {x},x\right)=0

은 때때로 ''가속도의 시간변화율 방정식''이라고 불린다. 3개의 1차 상미분 방정식계와 동등한 가속도의 시간변화율 방정식은 특정 의미에서 혼돈적 거동을 보이는 해에 대한 최소 설정임이 증명되었다. 이는 가속도의 시간변화율 시스템에 대한 수학적 관심을 불러일으킨다. 4차 또는 그 이상의 도함수를 포함하는 시스템은 하이퍼가속도의 시간변화율 시스템이라고 한다.^[54]

가속도의 시간변화율 시스템의 거동은 가속도의 시간변화율 방정식으로 설명되며, 특정 가속도의 시간변화율 방정식의 경우 간단한 전자 회로가 해를 모델링할 수 있다. 이러한 회로는 가속도의 시간변화율 회로로 알려져 있다.

가속도의 시간변화율 회로의 가장 흥미로운 특성 중 하나는 혼돈적 거동의 가능성이다. 사실, 로렌츠 어트랙터 및 뢰슬러 맵(Rössler map)과 같은 특정 잘 알려진 혼돈 시스템은 일반적으로 하나의 (다소 복잡한) 가속도의 시간변화율 방정식으로 결합될 수 있는 3개의 1차 미분 방정식 시스템으로 설명된다.

x

의 크기에 비선형성이 있는 가속도의 시간변화율 방정식의 또 다른 예는 다음과 같다.

:

\frac{\mathrm{d}^3 x}{\mathrm{d} t^3}+A\frac{\mathrm{d}^2 x}{\mathrm{d} t^2}+\frac{\mathrm{d} x}{\mathrm{d} t}-|x|+1=0.

여기서 ''A''는 조정 가능한 매개변수이다. 이 방정식은 ''A''=3/5일 때 혼돈적인 해를 가지며 다음 가속도의 시간변화율 회로로 구현할 수 있다. 필요한 비선형성은 두 개의 다이오드에 의해 발생한다.

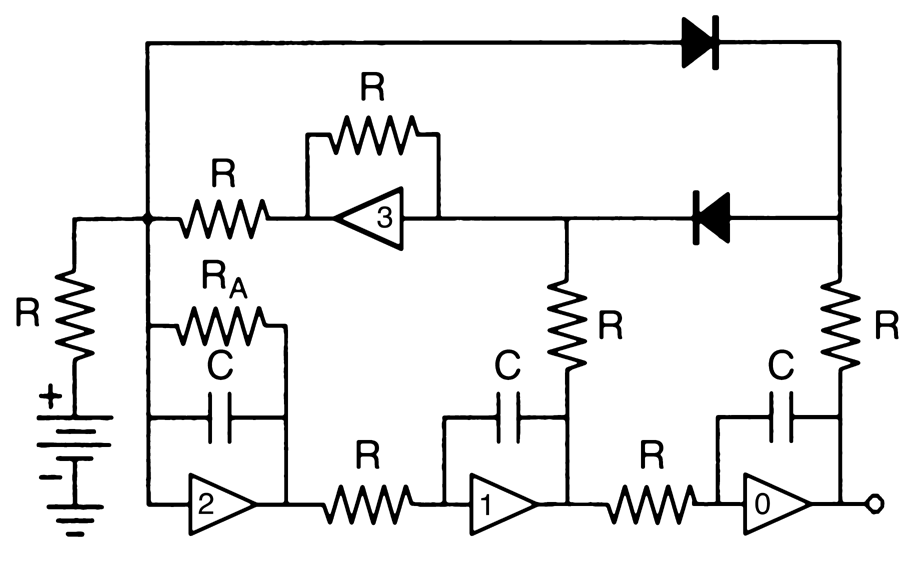
위 회로에서 모든 저항은

R_A=R/A=5R/3

을 제외하고 같은 값을 가지며, 모든 커패시터는 같은 크기를 갖는다. 주파수는

1/2\pi R C

이다. 연산 증폭기 0의 출력은 x 변수에 해당하고, 1의 출력은 x의 1차 도함수에 해당하며, 2의 출력은 2차 도함수에 해당한다.

유사한 회로는 하나의 다이오드^[55] 또는 다이오드가 전혀 필요하지 않다.^[56]

혼돈적 진정한 난수 생성기의 기초 중 하나인 잘 알려진 추아 회로(Chua's circuit)도 참조한다.^[57] 회로의 간편한 구성으로 인해 혼돈 시스템의 실제 세계의 보편적인 예가 되었다.

4. 응용

나비 효과로 잘 알려진 혼돈 현상은 지구의 대기, 판 구조론, 경제 및 인구 현상, 다중성계의 궤도 변화 등 다양한 자연 및 사회 현상에 응용된다.^[106] 혼돈 이론은 지질학, 수학, 생물학, 컴퓨터 과학, 경제학,^[107]^[108]^[109] 공학,^[110]^[111] 금융,^[112]^[113]^[114]^[115]^[116] 기상학, 철학, 인류학,^[15] 물리학,^[117]^[118]^[119] 정치학,^[120]^[121] 인구 역학,^[122] 로봇 공학 등 다양한 분야에 적용된다.^[131]^[132]

혼돈 이론은 암호학에서 암호 원시 함수 설계에 활용되며,^[123] 이미지 암호화, 해시 함수, 안전한 의사난수 생성기, 스트림 암호, 워터마킹, 스테가노그래피 등에 사용된다.^[124] DNA 컴퓨팅과 결합하여 이미지 및 정보 암호화에도 활용된다.^[126]

로봇 공학에서는 혼돈 이론을 사용하여 예측 모델을 구축하고, 수동 보행 이족 보행 로봇의 혼돈 역학을 연구한다.^[132]

생물학에서는 개체군 모델에 혼돈 이론을 적용하여 캐나다 스라소니 개체군 성장과 같은 혼돈적 행동을 연구하고,^[133] 수문학^[134] 및 태아심박측정술^[135]에도 응용된다. 생태학에서 혼돈 시계열 모델링은 실제 혼돈과 모델 혼돈을 구분하는 어려움이 있지만,^[136] 유전자 대 유전자 공진화는 대립 유전자 빈도에서 혼돈 역학을 보이기도 한다.^[1]

경제학에서는 혼돈 이론을 통해 경제 모델을 개선할 수 있지만, 경제 시스템의 복잡성으로 인해 정확한 예측은 어렵다.^[139] 재귀 양자화 분석을 통해 경제학에서 혼돈을 발견하고, 거시경제 변수 간의 차이점과 경제 역동성의 숨겨진 특징을 강조할 수 있다.^[142]

화학에서는 기체 용해도 예측에 혼돈 이론을 도입한 개선된 입자군 최적화(PSO) 모델이 개발되었고,^[148] 천체역학에서는 소행성 관측에 혼돈 이론을 적용하여 지구 접근 시점을 예측하며,^[149] 명왕성의 위성 회전 연구에도 활용된다. 양자물리학과 전기 공학에서는 다수의 조셉슨 접합 어레이 연구에 혼돈 이론이 사용되었다.^[150]

혼돈 이론은 자연 과학 외에도 적용되지만, 재현성 부족, 낮은 외부 타당성 등으로 인해 예측 정확도가 떨어지는 문제가 있다.^[152]^[153] 인간의 심장 박동, 동물 행동, 직업 상담 모델, 조직 및 팀워크 연구 등에도 혼돈 이론이 적용되거나 연구되었지만, 일부 연구에서는 한계점들이 발견되기도 하였다.^[154]^[155]^[156]^[157]

교통 예측에 혼돈 이론을 적용하여 교통 체증 발생 시점을 예측하고, 혼돈 이론과 다른 방법을 결합하여 정확한 단기 예측 모델을 만들 수 있다.^[158] 또한, 강우량과 하천 유량 등 환경 물 순환 데이터에도 적용되었지만,^[159] 논란의 여지가 있는 결과를 얻기도 하였다.^[160]

5. 역사

에드워드 노턴 로렌즈는 1961년에 기상학 컴퓨터 시뮬레이션을 연구하던 도중 로렌즈 방정식의 야릇한 끌개를 발견하였다.^[179] 제임스 클러크 맥스웰은 1860년대와 1870년대의 연구를 통해 "나비 효과"를 최초로 강조하며 초기 카오스 이론 논의자 중 한 명으로 여겨진다.^[60]^[61]^[62] 앙리 푸앵카레는 초기 카오스 이론 지지자 중 한 명이었다.

카오스 이론은 에르고딕 이론 분야에서 시작되었다. 이후 조지 데이비드 버코프^[67], 안드레이 콜모고로프^[68]^[69]^[70], 메리 루시 카트라이트와 존 에덴서 리틀우드^[71], 스티븐 스메일^[72]이 비선형 미분 방정식을 연구하였다. 1959년 보리스 발레리아노비치 치리코프는 해밀토니안 시스템에서 고전적 혼돈 발생 기준(치리코프 기준)을 제안하고, 열린 거울 트랩에서의 플라스마 밀폐 실험 결과를 설명하는 데 적용했다.^[73]^[74] 이는 구체적인 실험을 설명하는 데 성공한 최초의 물리적 혼돈 이론으로, 치리코프는 고전 및 양자 혼돈의 선구자로 여겨진다.^[75]^[76]^[77]

전자 컴퓨터는 카오스 이론 발전의 주요 촉매제였다. 간단한 수학 공식의 반복적인 반복을 포함하는 카오스 이론의 수학적 내용은 손으로 계산하기 비실용적이었으나, 전자 컴퓨터는 이러한 반복 계산을 실용적으로 만들었고 그림과 이미지를 통해 시스템을 시각화할 수 있게 했다.

카오스 게임으로 생성한 바른슬리 양치류. 양치류, 구름, 산 등 자연 형태는 반복 함수계(IFS)로 재현할 수 있다.

1963년 브누아 망델브로는 프랙털 기하학을 도입하여,^[180] 야릇한 끌개의 프랙털 성질을 규명하는 이론적 기반을 제공하였다. 1975년 리톈옌(Tien-Yien Li^영어)과 제임스 요크는 "혼돈"(chaos|케이오스^영어)이라는 용어를 전문 용어로 최초로 사용하였다.^[171] 이는 그리스 신화에서 우주 태초의 상태 (또는 그 의인화)를 뜻하는 χάος|카오스^grc에서 유래한다.

1976년 오토 에버하르트 뢰슬러(Otto Eberhard Rössler^de)는 연속 시간 혼돈계인 뢰슬러 끌개를 발표하였다.^[181] 1978년 미첼 파이겐바움은 파이겐바움 상수를 발견하였다.

1986년 뉴욕 과학 아카데미는 국립 정신 건강 연구소 및 해군 연구소와 공동으로 생물학 및 의학 분야의 카오스에 대한 최초의 중요한 회의를 공동 주최했고, 베르나르도 후버만은 정신분열증 환자의 안구 추적 기능 장애에 대한 수학적 모델을 제시했다.^[91] 1987년 퍼 박, 차오 탕, 쿠르트 비젠펠트는 ''피지컬 리뷰 레터스''^[92]에 복잡성이 자연에서 발생하는 메커니즘 중 하나로 간주되는 자기 조직 임계성(SOC)을 설명하는 논문을 처음 발표했다.

1987년 제임스 글릭은 대중 교양 서적 《카오스: 새로운 과학의 출현》(Chaos: Making a New Science^영어)을 출판하여 혼돈 이론을 대중화하였다.^[182]^[183]

5. 1. 19세기

앙리 푸앵카레는 1880년대에 삼체 문제를 연구하면서 비주기적이면서도 영원히 증가하지도 않고, 고정점에 도달하지도 않는 궤도가 있을 수 있다는 것을 발견했다.^[173] 이는 혼돈 이론의 기초를 마련한 중요한 발견이었다. 1892년 2차원에서는 혼돈이 일어날 수 없다는 푸앵카레-벤딕손 정리를 발표하였으나, 이에 대한 엄밀한 증명을 제시하지 않았다.^[173]

자크 아다마르는 1898년 종수 2의 리만 곡면 위의 측지선을 연구하면서, 이 동역학계가 양의 리야푸노프 지수를 갖는다는 것을 발견하였다.^[174] 이는 혼돈계의 특징을 보여주는 또 다른 중요한 발견이었다. 이후 이바르 오토 벤딕손이 1901년에 푸앵카레-벤딕손 정리를 엄밀하게 증명하였다.^[174]

제임스 클러크 맥스웰은 최초로 "나비 효과"를 강조했으며, 1860년대와 1870년대의 연구를 통해 초기 카오스 이론 논의자 중 한 명으로 여겨진다.^[60]^[61]^[62]

5. 2. 20세기 초

조지 데이비드 버코프는 혼돈과 밀접하게 연관된 에르고딕성을 연구하였고, 버코프 에르고딕 정리를 증명하였다.^[67] 안드레이 콜모고로프는 1941년에 유체 역학의 난류를 연구하였고,^[175] 1954년에 미세한 비선형성에 대한 콜모고로프-아르놀트-모저 정리를 도입하였다.^[176] 메리 카트라이트와 존 이든저 리틀우드는 1945년에 무선 공학에서 자연스럽게 등장하는 판데르폴 진동자를 연구하였다.^[177] 스티븐 스메일은 1960년에 비선형 동역학계를 모스 이론을 사용하여 분석하였다.^[178]

5. 3. 20세기 후반

에드워드 로렌츠는 1961년 날씨 예측 연구 중 로열 맥비 LGP-30 컴퓨터를 이용한 기상 시뮬레이션에서 초기 조건의 미세한 차이가 장기적인 결과에 큰 영향을 미치는 것을 발견했다.^[82] 이는 나비 효과로 알려지게 되었으며, 로렌츠 어트랙터라는 개념을 통해 상세한 대기 모델링으로도 정확한 장기 날씨 예측이 어렵다는 것을 보여주었다. 1963년에는 이 결과를 텐트 사상에 의해 발생하는 카오스로 발표하였다.^[168]

베누아 망델브로는 1963년 주가와 전화 회로 등에서 나타나는 잡음이 칸토르 집합처럼 패턴화되어 있다는 것을 발견하고,^[83] 1967년에는 영국의 해안선 길이에 대한 연구를 통해 프랙탈 개념을 제시했다.^[86] 1982년에는 ''자연의 프랙탈 기하학''을 출판하여 프랙탈 기하학을 카오스 이론의 중요한 부분으로 만들었다.^[87]

교토대학의 우에다 료는 1961년 전기 회로에서 발생하는 카오스를 관측하고 불규칙 천이 현상이라 명명했으며, 이는 후에 다비드 뤼엘에 의해 재패니즈 아트랙터로 알려지게 되었다.

1975년, 제임스 A. 요크와 리 티엔이엔은 복잡한 궤도의 개념을 "카오스"라고 명명했다.

1977년 12월, 뉴욕 과학 아카데미는 최초의 카오스 심포지엄을 개최하여 다비드 뤼엘, 로버트 메이, 제임스 A. 요크, 로버트 쇼, 에드워드 로렌츠 등이 참석했다.

1979년 알버트 J. 리브체이버는 레이리-베나르 대류 시스템에서 혼돈과 난류로 이어지는 분기 캐스케이드에 대한 실험적 관찰을 발표했고, 1986년 미첼 J. 파이겐바움과 함께 울프상 물리학상을 수상했다.^[90]

1987년, 제임스 글릭은 ''카오스: 새로운 과학 만들기''를 출판하여 카오스 이론을 대중에게 널리 알렸다.^[94]

참조

_[1] 웹사이트 chaology https://en.wiktionar[...] 2024-11-17
_[2] 웹사이트 chaos theory Definition & Facts https://www.britanni[...] 2019-11-24
_[3] 웹사이트 What is Chaos Theory? – Fractal Foundation https://fractalfound[...] 2019-11-24
_[4] 웹사이트 Chaos http://mathworld.wol[...] 2019-11-24
_[5] 웹사이트 Chaos Theory and the Logistic Map https://geoffboeing.[...] 2020-05-17
_[6] 서적 The Essence of Chaos https://books.google[...] University of Washington Press
_[7] 논문 Three Kinds of Butterfly Effects within Lorenz Models 2022-07-04
_[8] 서적 In the Wake of Chaos: Unpredictable Order in Dynamical Systems https://archive.org/[...] University of Chicago Press
_[9] 백과사전 Chaos https://plato.stanfo[...] Metaphysics Research Lab, Stanford University 2019-11-24
_[10] 서적
_[11] 서적
_[12] 논문 What are the New Implications of Chaos for Unpredictability?
_[13] 웹사이트 Chaos in an Atmosphere Hanging on a Wall http://mpe.dimacs.ru[...] 2018-06-12
_[14] 서적 Complex nonlinearity: chaos, phase transitions, topology change, and path integrals Springer
_[15] 서적 On the order of chaos. Social anthropology and the science of chaos Berghahn Books
_[16] 웹사이트 Covid-19 Pandemic and Chaos Theory: Applications based on a Bibliometric Analysis https://www.research[...] 2020-05-13
_[17] 서적 Everyday Chaos – Technology, Complexity and How We're Thriving in a New World of Possibility https://books.google[...] Harvard Business Review Press
_[18] 논문 Chaotic Evolution of the Solar System 1992-07-03
_[19] 서적 Sync: The Emerging Science of Spontaneous Order Hyperion
_[20] 웹사이트 chaos
_[21] 웹사이트 Definition of chaos Dictionary.com https://www.dictiona[...] 2019-11-24
_[22] 서적 A First Course in Dynamics: With a Panorama of Recent Developments Cambridge University Press
_[23] 서적 Discrete Chaos Chapman & Hall/CRC
_[24] 서적 Topology and its applications Wiley
_[25] 논문 On Devaney's definition of chaos 1992
_[26] 논문 On Intervals, Transitivity = Chaos 1994-04
_[27] 서적 Nonlinear Dynamics: A Primer https://archive.org/[...] Cambridge University Press
_[28] 웹사이트 Edward Lorenz, father of chaos theory and butterfly effect, dies at 90 http://news.mit.edu/[...] 2019-11-24
_[29] 논문 One Saddle Point and Two Types of Sensitivities within the Lorenz 1963 and 1969 Models 2022-05-07
_[30] 서적 Global Warming and the Future of the Earth https://archive.org/[...] Morgan & Claypool
_[31] 웹사이트 Lyapunov Characteristic Exponent http://mathworld.wol[...] 2019-11-24
_[32] 서적
_[33] 서적
_[34] 서적
_[35] 논문 Period Three Implies Chaos http://pb.math.univ.[...]
_[36] 논문 Medium-Term Prediction of Chaos 2006
_[37] 논문 Metastable chaos: The transition to sustained chaotic behavior in the Lorenz model https://doi.org/10.1[...] 1979-09-01
_[38] 서적 13th Chaotic Modeling and Simulation International Conference Springer International Publishing 2021
_[39] 논문 The Dual Nature of Chaos and Order in the Atmosphere 2022-11-12
_[40] 논문 Simplest dissipative chaotic flow 1997
_[41] 논문 Non-chaotic behaviour in three-dimensional quadratic systems 1997
_[42] 논문 Nonchaotic behaviour in three-dimensional quadratic systems II. The conservative case 1999
_[43] 논문 Slow chaos in surface flows http://link.springer[...] 2021
_[44] 논문 A Banach space which admits no chaotic operator 2001
_[45] 논문 Nonlinear Feedback in a Five-Dimensional Lorenz Model https://journals.ame[...] 2014-05-01
_[46] 논문 The onset of chaos in nonlinear dynamical systems determined with a new fractal technique https://www.worldsci[...] 2005-03-01
_[47] 논문 Generalized Lorenz models and their routes to chaos. I. Energy-conserving vertical mode truncations https://www.scienced[...] 2007-05-01
_[48] 논문 Aggregated Negative Feedback in a Generalized Lorenz Model 2019-03-01
_[49] 논문 Is Weather Chaotic?: Coexistence of Chaos and Order within a Generalized Lorenz Model 2021-01-01
_[50] 논문 Solitary waves as fixed points of infinite-dimensional maps for an optical bistable ring cavity: Analysis 1988
_[51] 서적 Proceedings of the Lebedev Physics Institute Nauka 1988
_[52] 논문 Spatial soliton laser: geometry and stability 2000
_[53] 논문 Structured light entities, chaos and nonlocal maps 2020
_[54] 논문 Chaotic Hyperjerk Systems http://sprott.physic[...] 2005
_[55] 논문 A New Chaotic Jerk Circuit http://sprott.physic[...] 2011
_[56] 논문 Simple Autonomous Chaotic Circuits http://sprott.physic[...] 2010
_[57] 논문 Secure Image Encryption Based On a Chua Chaotic Noise Generator http://www.jestr.org[...] 2013
_[58] 서적 Sync: The Emerging Science of Spontaneous Order Hyperion 2003
_[59] 논문 Ubiquitous order known as chaos https://www.scienced[...] 2024-02-15
_[60] 논문 Maxwell on Chaos https://yorke.umd.ed[...] 1993
_[61] 웹사이트 James Clerk Maxwell: a force for physics https://physicsworld[...] 2006-12-01
_[62] 논문 Chaos theory and applications: a retrospective on lessons learned and missed or new opportunities 2020-10-01
_[63] 논문 Sur le problème des trois corps et les équations de la dynamique. Divergence des séries de M. Lindstedt 1890
_[64] 서적 The three-body problem and the equations of dynamics : Poincaré's foundational work on dynamical systems theory Springer International Publishing 2017
_[65] 서적 Celestial Encounters: The Origins of Chaos and Stability Princeton University Press 1996
_[66] 논문 Les surfaces à courbures opposées et leurs lignes géodesiques 1898
_[67] 서적 Dynamical Systems American Mathematical Society 1927
_[68] 논문 Local structure of turbulence in an incompressible fluid for very large Reynolds numbers 1941
_[69] 논문 On degeneration of isotropic turbulence in an incompressible viscous liquid 1941
_[70] 서적 Stochastic Behavior in Classical and Quantum Hamiltonian Systems 1979
_[71] 논문 On non-linear differential equations of the second order, I: The equation ''y''" + ''k''(1−''y''²)''y''' + ''y'' = ''b''λkcos(λ''t'' + ''a''), ''k'' large
_[72] 논문 Morse inequalities for a dynamical system 1960-01-01
_[73] 논문 РЕЗОНАНСНЫЕ ПРОЦЕССЫ В МАГНИТНЫХ ЛОВУШКАХ https://www.quantwar[...]
_[74] 논문 Resonance processes in magnetic traps https://doi.org/10.1[...] 1960-12-01
_[75] 논문 Boris Chirikov, a pioneer in classical and quantum chaos https://www.quantwar[...] 1998-02-27
_[76] 논문 A pioneer of chaos http://dx.doi.org/10[...] 1999-07-01
_[77] 서적 Chaos at Fifty Four in 2013 http://worldcat.org/[...]
_[78] harvnb
_[79] harvnb https://books.google[...]
_[80] 논문 Deterministic non-periodic flow
_[81] 웹사이트 The Hidden Heroines of Chaos https://www.quantama[...] 2019-05-20
_[82] 서적 Chaos: Making a New Science Cardinal
_[83] 논문 A new model for error clustering in telephone circuits
_[84] 서적 The Fractal Geometry of Nature Freeman
_[85] 서적 The (Mis)behavior of Markets: A Fractal View of Risk, Ruin, and Reward https://archive.org/[...] Basic Books
_[86] 논문 How Long Is the Coast of Britain? Statistical Self-Similarity and Fractional Dimension http://ena.lp.edu.ua[...] 1967-05-05
_[87] 서적 The Fractal Geometry of Nature https://archive.org/[...] Macmillan 1982
_[88] 논문 Quantitative universality for a class of nonlinear transformations 1978-07-01
_[89] 논문 Iterations d'endomorphismes et groupe de renormalisation
_[90] 웹사이트 The Wolf Prize in Physics in 1986. http://www.wolffund.[...]
_[91] 논문 A Model for Dysfunctions in Smooth Pursuit Eye Movement 1987-07-01
_[92] 논문 Self-organized criticality: An explanation of the 1/f noise 1987-07-27
_[93] 논문 On the aftershocks of earthquakes
_[94] 서적 Chaos: Making a New Science Penguin Books 2008-08-26
_[95] 논문 Chaos at fifty http://www.physicsto[...]
_[96] 논문 Managing chaos: Thinking out of the box 2007-01-01
_[97] 서적 Chaos Theory in the Social Sciences: Foundations and Applications University of Michigan Press 1996-01-01
_[98] 웹사이트 Butterfly Effect and Chaos. https://www.ee.cityu[...] 2020-01-01
_[99] 논문 The 50th Anniversary of the Metaphorical Butterfly Effect since Lorenz (1972): Multistability, Multiscale Predictability, and Sensitivity in Numerical Models. 2023-08-12
_[100] 논문 A Review of Lorenz's Models from 1960 to 2008 https://doi.org/10.1[...] 2023-09-04
_[101] 논문 The problem of deducing the climate from the governing equations. 1964-01-01
_[102] 서적 50th Anniversary of the Metaphorical Butterfly Effect since Lorenz (1972): Multistability, Multiscale Predictability, and Sensitivity in Numerical Models MDPI 2023-10-11
_[103] 웹사이트 The butterfly effect. In Premio Felice Pietro Chisesi E Caterina Tomassoni Award Lecture; University of Rome: Rome, Italy. https://eapsweb.mit.[...] 2008-12-01
_[104] 웹사이트 A Popular but Inaccurate Analogy for Chaos and Butterfly Effect https://www.youtube.[...] 2023-02-20
_[105] 논문 Can the Flap of a Butterfly's Wings Shift a Tornado into Texas—Without Chaos? 2023-05-02
_[106] 웹사이트 The Geometry and Pigmentation of Seashells https://www.maths.no[...] University of Nottingham 2009-02-01
_[107] 논문 Evidence for chaotic dependence between US inflation and commodity prices
_[108] 논문 Detecting positive feedback in multivariate time series: the case of metal prices and US inflation
_[109] 서적 New Trends in Macroeconomics Springer Verlag
_[110] 논문 Chaotic signatures of photoconductive Cu 2 ZnSnS 4 nanostructures explored by Lorenz attractors 2018-01-01
_[111] 웹사이트 Applying Chaos Theory to Embedded Applications http://www.dspdesign[...]
_[112] 논문 Evidence for nonlinear asymmetric causality in US inflation, metal and stock returns
_[113] 논문 Is it possible to study chaotic and ARCH behaviour jointly? Application of a noisy Mackey-Glass equation with heteroskedastic errors to the Paris Stock Exchange returns series
_[114] 서적 Trading Chaos: Maximize Profits with Proven Technical Techniques Wiley
_[115] 서적 Fractal market analysis : applying chaos theory to investment and economics Wiley
_[116] 서적 Chaos and order in the capital markets : a new view of cycles, prices, and market volatility John Wiley & Sons
_[117] 논문 Guiding a self-adjusting system through chaos 2007-01-01
_[118] 논문 Chaos in a one-dimensional compressible flow 2007-01-01
_[119] 논문 Adaptation to the Edge of Chaos in the Self-Adjusting Logistic Map 2009-01-01
_[120] 논문 Challenges of Instability: The Concepts of Synergetics in Studying the Historical Development of Russia 2019-01-01
_[121] 서적 Chaos, complexity and leadership 2018 explorations of chaotic and complexity theory Springer 2018-01-01
_[122] 논문 Periodic and Quasi-Periodic Behavior in Resource Dependent Age Structured Population Models
_[123] 논문 A symmetric image encryption scheme based on combination of nonlinear chaotic maps 2011-10-01
_[124] 논문 A novel algorithm for image encryption based on mixture of chaotic maps 2008-01-01
_[125] 논문 An improved key agreement protocol based on chaos
_[126] 논문 A novel text and image encryption method based on chaos theory and DNA computing
_[127] 논문 Cryptanalysis of an image encryption algorithm based on DNA encoding 2017-10-01
_[128] 논문 Cryptanalysis of an Image Encryption Algorithm Based on DNA Sequence Operation and Hyper-chaotic System 2017-06-01
_[129] 논문 Cryptanalyzing a RGB image encryption algorithm based on DNA encoding and chaos map 2014-08-01
_[130] 논문 Quantitative description of robot–environment interaction using chaos theory http://cswww.essex.a[...] 2005-12-01
_[131] 논문 A Study of the Passive Gait of a Compass-Like Biped Robot: Symmetry and Chaos
_[132] 논문 Chaos in discrete structured population models
_[133] 논문 Comparison study of AR models on the Canadian lynx data: a close look at BDS statistic
_[134] 논문 Chaos theory in hydrology: important issues and interpretations 2000-01-31
_[135] 논문 Chaos theory and power spectrum analysis in computerized cardiotocography 1997-02-01
_[136] 서적 Chaos in Real Data : The Analysis of Non-Linear Dynamics from Short Ecological Time Series Springer Science+Business Media Dordrecht
_[137] 논문 Gene-for-gene coevolution between plants and parasites Nature Publishing Group
_[138] 서적 The Epidemiology of Plant Diseases Springer Science+Business Media Dordrecht
_[139] 논문 Applying the theory of chaos and a complex model of health to establish relations among financial indicators
_[140] 논문 Chaos in foreign exchange markets: a sceptical view http://centaur.readi[...]
_[141] 저널 RQA correlations on real business cycles time series 2017-12-18
_[142] 저널 Recurrence quantification analysis of business cycles https://www.scienced[...] 2018-05-01
_[143] 저널 Business cycle modeling between financial crises and black swans: Ornstein–Uhlenbeck stochastic process vs Kaldor deterministic chaotic model https://aip.scitatio[...] 2020-08-01
_[144] 서적 The Feasibility of a Global Observation and Analysis Experiment http://dx.doi.org/10[...] 1966-01-01
_[145] 저널 GARP topics
_[146] 저널 Exploring the Origin of the Two-Week Predictability Limit: A Revisit of Lorenz's Predictability Studies in the 1960s 2024-07-16
_[147] arXiv The Butterfly Effect of Altering Prompts: How Small Changes and Jailbreaks Affect Large Language Model Performance 2024-01-01
_[148] 저널 Prediction of gas solubility in polymers by back propagation artificial neural network based on self-adaptive particle swarm optimization algorithm and chaos theory 2013-10-25
_[149] 저널 Chaotic diffusion in celestial mechanics
_[150] 서적 Sync: The Emerging Science of Spontaneous Order Hyperion
_[151] 저널 Prediction method for risks of coal and gas outbursts based on spatial chaos theory using gas desorption index of drill cuttings 2011-05
_[152] 서적 The impact of chaos on science and society United Nations University Press
_[153] 서적 The impact of chaos on science and society United Nations University Press
_[154] 저널 Chaotic dynamics in autonomic nervous system activity of a patient during a psychotherapy session 1992
_[155] 서적 Chaos theory in psychology Greenwood Press
_[156] 저널 Probabilities and Possibilities: The Strategic Counseling Implications of the Chaos Theory of Careers 2008-06
_[157] 저널 An examination of initiation rituals in a UK sporting institution and the impact on group development 2018
_[158] 저널 Short-term traffic speed forecasting hybrid model based on Chaos–Wavelet Analysis-Support Vector Machine theory 2013-02
_[159] 웹사이트 Dr. Gregory B. Pasternack – Watershed Hydrology, Geomorphology, and Ecohydraulics :: Chaos in Hydrology http://pasternack.uc[...] 2017-06-12
_[160] 저널 Does the river run wild? Assessing chaos in hydrological systems 1999-11-01
_[161] 웹사이트 Chaos http://mathworld.wol[...] Wolfram Research 2014-12-11
_[162] 저널 On_Devaney's_Definition_of_Chaos https://www.research[...] Mathematical Association of America 2020-07-25
_[163] 웹사이트 Matter and motion pp.13-14 https://archive.org/[...] University of California Libraries 2014-12-10
_[164] 웹사이트 복잡한 현상에 맞서는 현대 물리학 다양성에 숨겨진 “일”의 불변성 Chap.2 http://elekitel.jp/e[...] 東芝 2014-12-10
_[165] 간행물 Sur le probleme des trois corps et les equations de la dynamique. Divergence des series de M. Lindstedt
_[166] 서적 Celestial Encounters: The Origins of Chaos and Stability Princeton University Press
_[167] 간행물 Frequency demultiplication
_[168] 저널 Deterministic non-periodic flow
_[169] 기타
_[170] 기타
_[171] 저널 Period Three Implies Chaos 1975-12
_[172] 저널 Сосуществование циклов непрерывного преобразования прямой в себя 1964
_[173] 간행물 Sur les courbes définies par une équation différentielle
_[174] 저널 Sur les courbes définies par des équations différentielles
_[175] 저널 Локальная структура турбулентности в несжимаемой вязкой жидкости при очень больших числах Рейнольдса http://ufn.ru/ru/art[...]
_[176] 저널 Preservation of conditionally periodic movements with small change in the Hamiltonian function
_[177] 저널 On non-linear differential equations of the second order, I: The equation $\ddot y-k(1-y^2)\dot y+y=b\lambda k\cos(\lambda t+a)$ , $k$ large
_[178] 저널 Morse inequalities for a dynamical system 1960-01-01
_[179] 저널 Deterministic non-periodic flow
_[180] 저널 The variation of certain speculative prices https://archive.org/[...] 1963-01-01
_[181] 저널 An equation for continuous chaos
_[182] 서적 Chaos: Making a New Science http://www.around.co[...] Viking Books 1987-10-29
_[183] 서적 카오스: 새로운 과학의 출현 동아시아 2013-01-01